|
|
|
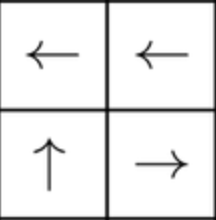
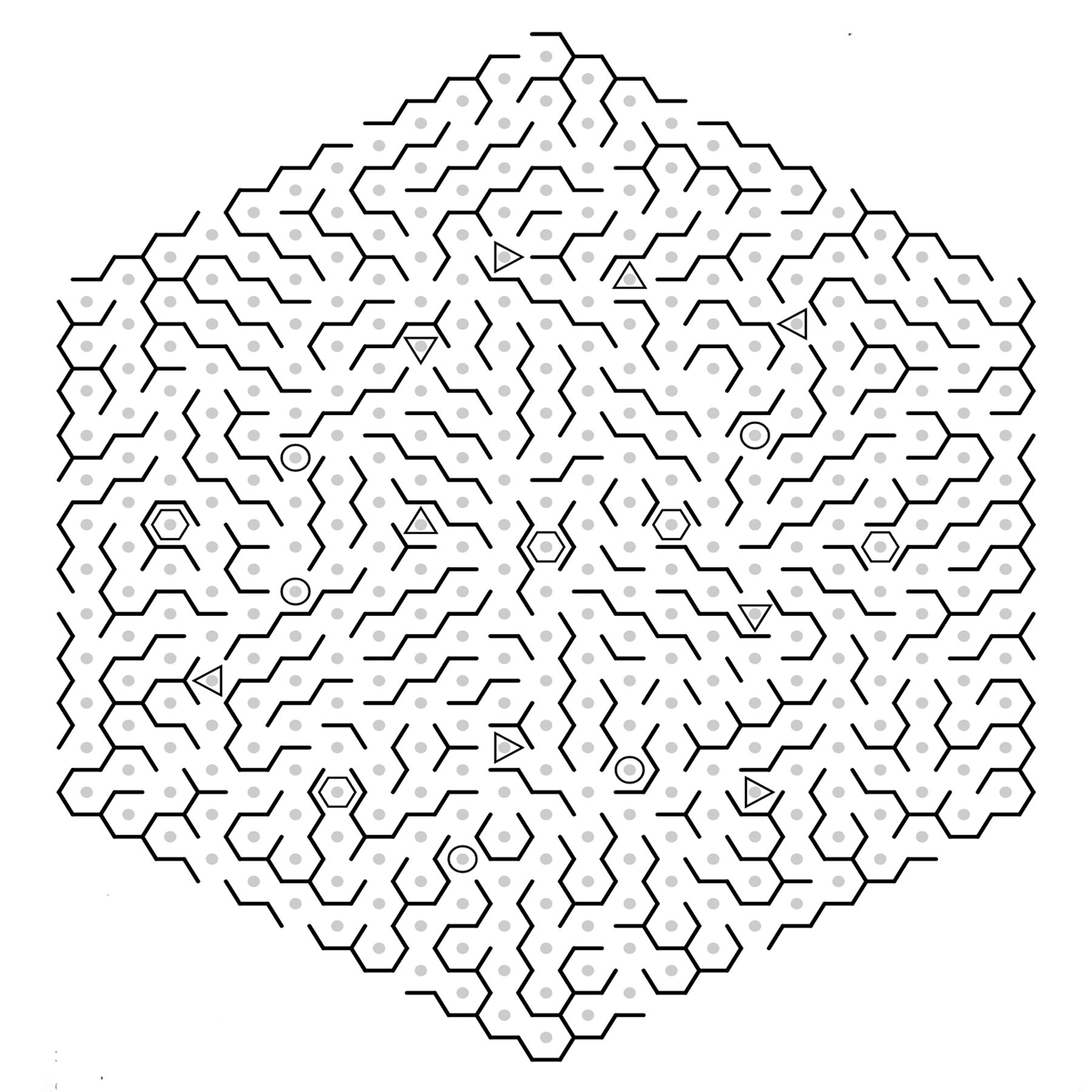
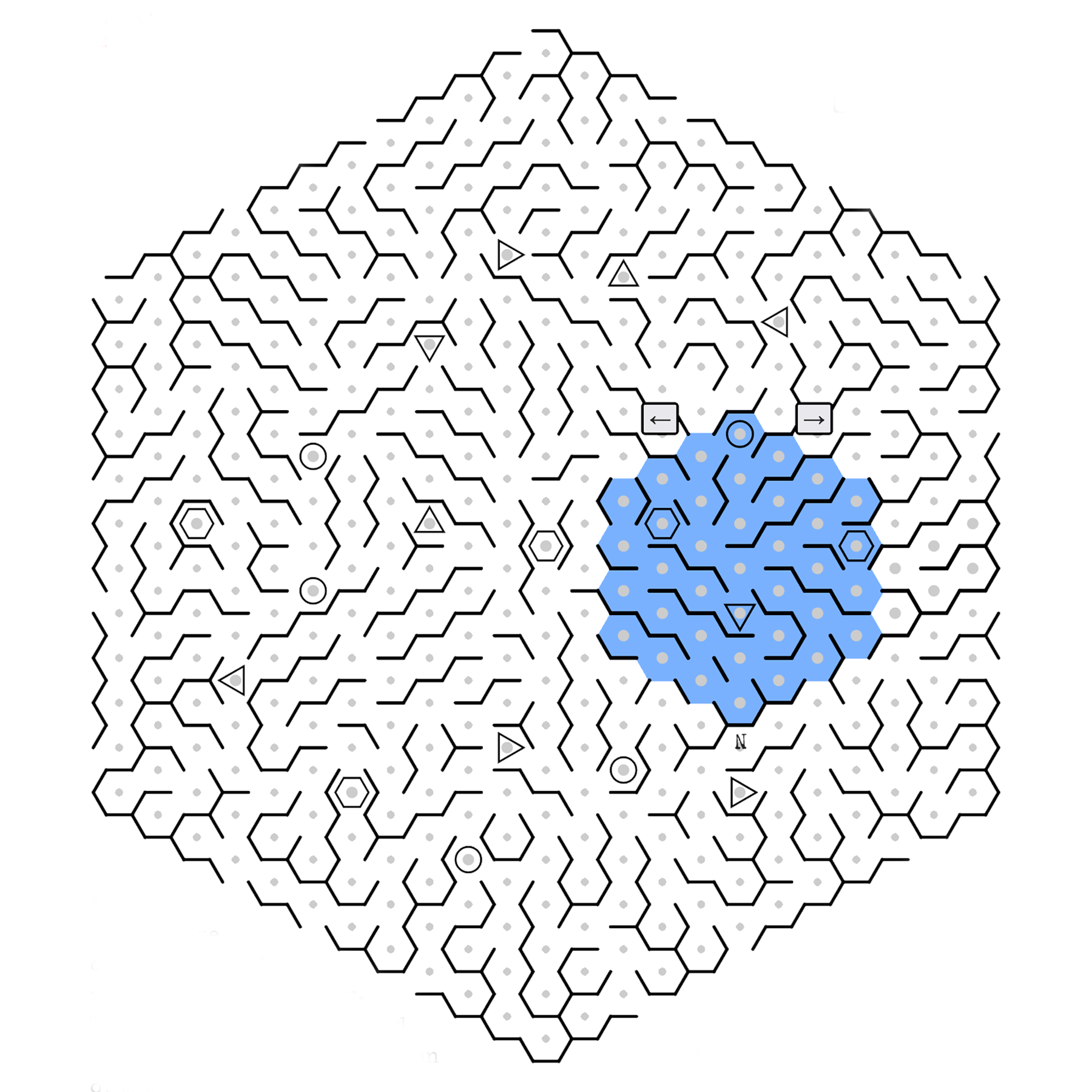
| What the defuser sees | What the manual user sees | The subgrid properly alligned to the large grid |

|

|

|
| What the defuser sees | What the manual user sees | The subgrid properly alligned to the large grid |